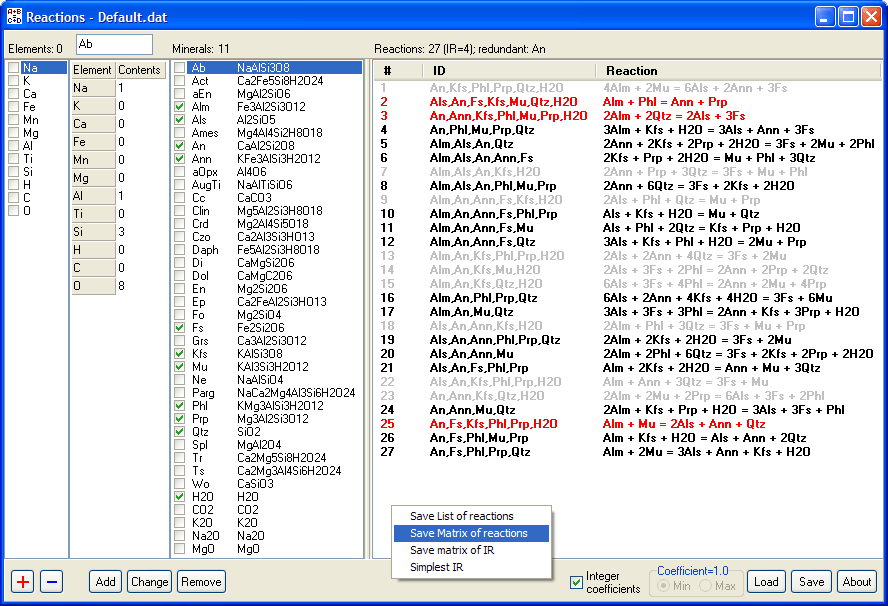
 Reactions: the program for generation of all possible reactions between specified substances and selection of arbitrary sets of linearly independent reactions
Reactions: the program for generation of all possible reactions between specified substances and selection of arbitrary sets of linearly independent reactions
Reactions is a small handy freeware for generation of all possible reactions between specified substances (pure minerals and components of solid solutions, oxides and chemical elements) with selection of the arbitrary set of linearly independent reactions. This program may be useful for education, for analysis of diagrams (petrogenetic grids and results of multi-equilibrium geothermobarometry), for balancing of reactions involving minerals with real compositions, for evaluation of solid solution end-members, etc.
The general approach is a sequence of relatively simple procedures that has been described in many publications (for example, in the chapter 5 of Frank Spear's monography Metamorphic Phase Equilibria and Pressure-Temperature-Time Paths (1993) or in the web-tutorial of Dexter Perkins at Teaching Phase Equilibria) and used in such programs as TWQ (Berman, 1991) and THERMOCALC (Powell & Holland, 1988). Nevertheless, I've decided to give a detailed description of this important algorithm. The description is accompanied by a rather complicated example of the system comprising almandine (Alm), sillimanite (Sill), annite (Ann), ferrosilite (Fs), muscovite (Mu), phlogopite (Phl), pyrope (Prp) and quartz (Qtz).
Calculation of reactions is performed in several stages.
First of all, let's write a compositional matrix for all the substances that may be involved in the reactions:
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Fe | 3 | 0 | 3 | 2 | 0 | 0 | 0 | 0
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| Al | 2 | 2 | 1 | 0 | 3 | 1 | 2 | 0
|
|---|
| Si | 3 | 1 | 3 | 2 | 3 | 3 | 3 | 1
|
|---|
| H | 0 | 0 | 2 | 0 | 2 | 2 | 0 | 0
|
|---|
| O | 12 | 5 | 12 | 6 | 12 | 12 | 12 | 2
|
|---|
Then transform it to the so-called
Reduced Row-Echelon Form (RREF) by the Gauss-Jordan elimination method. However, let's modify a little the commonly used procedure to produce the trapezoidal matrix with the left square identity part (with "1" on the main diagonal and "0" in other cells) and deleted zero rows (which correspond to linearly dependent elements). You can find the Pascal implementation in the documentation.
All the matrix transformations are based on elementary equivalent operations:
- Swapping of rows and columns
- Multiplication of a row by a constant
- Addition of rows
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 1 | 0.667 | 0 | 0 | 0 | 0 | Fe/3, moved up
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| Al | 0 | 2 | ‑1 | ‑1.333 | 3 | 1 | 2 | 0 | Al-Fe*2
|
|---|
| Si | 0 | 1 | 0 | 0 | 3 | 3 | 3 | 1 | Si-Fe*3
|
|---|
| H | 0 | 0 | 2 | 0 | 2 | 2 | 0 | 0
|
|---|
| O | 0 | 5 | 0 | -2 | 12 | 12 | 12 | 2 | O-Fe*12
|
|---|
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 1 | 0.667 | 0 | 0 | 0 | 0
|
|---|
| Al | 0 | 1 | ‑0.5 | ‑0.667 | 1.5 | 0.5 | 1 | 0 | Al/2, moved up
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| Si | 0 | 0 | 0.5 | 0.667 | 1.5 | 2.5 | 2 | 1 | Si-Al
|
|---|
| H | 0 | 0 | 2 | 0 | 2 | 2 | 0 | 0
|
|---|
| O | 0 | 0 | 2.5 | 1.333 | 4.5 | 9.5 | 7 | 2 | O-Al*5
|
|---|
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 0 | 0.667 | ‑1 | ‑1 | 0 | 0 | Fe-K
|
|---|
| Al | 0 | 1 | 0 | ‑0.667 | 2 | 1 | 1 | 0 | Al+K/2
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| Si | 0 | 0 | 0 | 0.667 | 1 | 2 | 2 | 1 | Si-K/2
|
|---|
| H | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | H-K*2, deleted
|
|---|
| O | 0 | 0 | 0 | 1.333 | 2 | 7 | 7 | 2 | O-K*2.5
|
|---|
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 0 | 0 | ‑2 | ‑3 | ‑2 | ‑1 | Fe-Si/3*2
|
|---|
| Al | 0 | 1 | 0 | 0 | 3 | 3 | 3 | 1 | Al+Si/3*2
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Si | 0 | 0 | 0 | 1 | 1.5 | 3 | 3 | 1.5 | Si*3/2, moved up
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| O | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0 | O-Si/3*4
|
|---|
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | Phl moved to the left
|
|---|
| Fe | 1 | 0 | 0 | 0 | ‑3 | ‑2 | ‑2 | ‑1
|
|---|
| Al | 0 | 1 | 0 | 0 | 3 | 3 | 3 | 1
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Si | 0 | 0 | 0 | 1 | 3 | 1.5 | 3 | 1.5
|
|---|
| Mg | 0 | 0 | 0 | 0 | 3 | 0 | 3 | 0
|
|---|
| O | 0 | 0 | 0 | 0 | 3 | 0 | 3 | 0
|
|---|
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 0 | 0 | 0 | ‑2 | 1 | ‑1 | Fe+Mg*3
|
|---|
| Al | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 1 | Al-Mg*3
|
|---|
| K | 0 | 0 | 1 | 0 | 0 | 1 | ‑1 | 0 | K-Mg
|
|---|
| Si | 0 | 0 | 0 | 1 | 0 | 1.5 | 0 | 1.5 | Si-Mg*3
|
|---|
| Mg | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | Mg/3
|
|---|
| O | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | O-Mg*3, deleted
|
|---|
The resulting trapezoidal matrix consists of only linearly independent rows (elements), its left part is a strict identity matrix and the right rectangular part contains calculated coefficients for some set of linearly independent reactions (with 3 reactions in this case):
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 0 | 0 | 0 | ‑2 | 1 | ‑1
|
|---|
| Al | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 1
|
|---|
| K | 0 | 0 | 1 | 0 | 0 | 1 | ‑1 | 0
|
|---|
| Si | 0 | 0 | 0 | 1 | 0 | 1.5 | 0 | 1.5
|
|---|
| Mg | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0
|
|---|
Thus, to get the matrix of coefficients of these independent reactions we should simply transpose the right rectangular part and augment it by the negative identity matrix at the right side:
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz
|
|---|
| ‑2 | 3 | 1 | 1.5 | 0 | ‑1 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑1 | 1 | 0 | 1.5 | 0 | 0 | 0 | ‑1
|
The same matrix with integer coefficients (after multiplication by appropriate constants):
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0 | 1 | 4Alm+2Mu=6Sill+2Ann+3Fs | (Phl,Prp,Qtz)
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0 | 2 | Ann+Prp=Alm+Phl | (Sill,Fs,Mu,Qtz)
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2 | 3 | 2Alm+2Qtz=2Sill+3Fs | (Ann,Phl,Mu,Prp)
|
All the following calculations use only this matrix with coefficients of linearly independent reactions: all other (dependent) reactions are different combinations of this small set.
The last column of this table contains lists of substances not involved in reactions: it is a commonly accepted notation for reactions in complex systems (the "ID" of reaction). It should be noted that this notation plays a key role at generation of dependent reactions because calculations are based on reduction of coefficients to zero just for absent substances.
As we can conclude from inspection of the compositional matrix transformed to RREF, the maximum number of substances M involved in any reaction should be more than the number of independent elements (rows) E by 1, i.e. M=E+1 (M=5+1=6 for this example system). Therefore, the number of absent substances N can not be less than total number of substances Q minus this maximum number of reaction substances M, i.e. N=Q-E-1 (N=8-5-1=2 for this example system).
The procedure for generation of reactions is based on evaluation of all possible combinations by N substances in the set of Q substances. The total number of such combinations C can be estimated using the formula:
$$C = \frac{Q!}{M! \times N!}$$
Thus, we should evaluate and check 28 combinations (by 2 substances in the set of 8 substances) for our example system. However, all linearly independent reactions have got numbers of absent substances (N) >2 (3 and 4) because of so-called degeneracy: elimination of some substances due to appropriate stoichiometric relationships. Degeneracy leads to correspondence of several combinations to a single reaction, i.e. the number of possible dependent reactions should be (essentially) less than the total number of combinations. At the same time, it's not necessary to calculate reaction coefficients for every generated combination: just check whether its set of absent substances is a subset of the analogous set for one of already calculated reactions. If so, this combination can be skipped. Therefore every reaction record should also contain some data structure and functionality for effective operations with sets (e.g. based on bit masks).
Calculation of reaction coefficients is performed by transformation of the matrix of linearly independent reactions: placing of columns with absent substances to its left side and reducing to a trapezoidal matrix by the Gauss elimination method. This method differs a bit from the Gauss-Jordan method used before: the left part of the resulting matrix is not a strict identity matrix, i.e. values on the main diagonal are not necessarily "1" and values above the main diagonal are not necessarily "0" (it is just an upper triangular matrix). The first values of the last row in this matrix will be nullified, i.e. the last row will contain coefficients of searched reaction (which you can convert to integers). The first step can be optimized if array with numbers of columns is used (to avoid moving whole columns).
So, let's calculate all the remaining linearly dependent reactions in our system:
| Combination | Absent substances | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| 1 | (Alm,Sill) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| -2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | 0 | ‑1.333 | 2 | 0.667 | 0.667 | ‑0.667 | ‑2
|
|
| 0 | 0 | ‑2 | 3 | 1 | 1 | ‑1 | ‑3 | 4 | 2Ann+Prp+3Qtz=3Fs+Phl+Mu | (Alm,Sill)
|
| Combination | Absent substances | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| 2 | (Alm,Ann) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑4 | 0 | 0 | ‑2 | 2 | 2 | ‑2
|
|
| 0 | ‑2 | 0 | 0 | ‑1 | 1 | 1 | ‑1 | 5 | 2Sill+Phl+Qtz=Mu+Prp | (Alm,Ann,Fs)
|
|
| 3 | (Alm,Fs) – subset of reaction #5
|
| Combination | Absent substances | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| 4 | (Alm,Phl) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| 0 | ‑2 | ‑2 | 3 | 0 | 2 | 0 | ‑4 | 6 | 2Sill+2Ann+4Qtz=3Fs+2Mu | (Alm,Phl,Prp)
|
| Combination | Absent substances | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| 5 | (Alm,Mu) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | 2 | ‑2 | 3 | 2 | 0 | ‑2 | ‑2 | 7 | 2Ann+2Prp+2Qtz=2Sill+3Fs+2Phl | (Alm,Mu)
|
|
| 6 | (Alm,Prp) – subset of reaction #6
|
| Combination | Absent substances | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| 7 | (Alm,Qtz) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
|
| 0 | 6 | ‑2 | 3 | 4 | ‑2 | ‑4 | 0 | 8 | 2Ann+2Phl+4Prp=6Sill+3Fs+4Phl | (Alm,Qtz)
|
| Combination | Absent substances | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| 8 | (Sill,Ann) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑0.667 | 0 | ‑0.667 | 2 | 0 | 0.667 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑1.333 | 0 | 0 | 2 | ‑0.667 | 0.667 | 0.667 | ‑2
|
|
| ‑2 | 0 | 0 | 3 | ‑1 | 1 | 1 | ‑3 | 9 | 2Alm+Phl+3Qtz=3Fs+Mu+Prp | (Sill,Ann)
|
|
| 9 | (Sill,Fs) – subset of reaction #2
|
| Combination | Absent substances | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| 10 | (Sill,Phl) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑0.667 | 0 | ‑0.667 | 2 | 0 | 0.667 | 0 | ‑2
|
|
| ‑1 | 0 | ‑1 | 3 | 0 | 1 | 0 | ‑3 | 10 | Alm+Ann+3Qtz=3Fs+Mu | (Sill,Phl,Prp)
|
|
| 11 | (Sill,Mu) – subset of reaction #2
|
| 12 | (Sill,Prp) – subset of reaction #10
|
| 13 | (Sill,Qtz) – subset of reaction #2
|
| 14 | (Ann,Fs) – subset of reaction #5
|
| 15 | (Ann,Phl) – subset of reaction #3
|
| 16 | (Ann,Mu) – subset of reaction #3
|
| 17 | (Ann,Prp) – subset of reaction #3
|
| Combination | Absent substances | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| 18 | (Ann,Qtz) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| ‑1 | 3 | 0 | 1.5 | 1 | ‑1 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
| ‑1 | 3 | 0 | 1.5 | 1 | ‑1 | ‑1 | 0
|
|
| ‑2 | 6 | 0 | 3 | 2 | ‑2 | ‑2 | 0 | 11 | 2Alm+2Mu+2Prp=6Sill+3Fs+2Phl | (Ann,Qtz)
|
| Combination | Absent substances | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | # | Reaction | Absent substances
|
|---|
| 19 | (Fs,Phl) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| 2 | ‑4 | ‑2 | 0 | 0 | 2 | 0 | ‑2
|
|
| 1 | ‑2 | ‑1 | 0 | 0 | 1 | 0 | ‑1 | 12 | 2Sill+Ann+Qtz=Alm+Mu | (Fs,Phl,Prp)
|
|
| 20 | (Fs,Mu) – subset of reaction #2
|
| 21 | (Fs,Prp) – subset of reaction #12
|
| 22 | (Fs,Qtz) – subset of reaction #2
|
| 23 | (Phl,Mu) – subset of reaction #3
|
| 24 | (Phl,Prp) – subset of reaction #10
|
| 25 | (Phl,Qtz) – subset of reaction #1
|
| 26 | (Mu,Prp) – subset of reaction #3
|
| 27 | (Mu,Qtz) – subset of reaction #2
|
| 28 | (Prp,Qtz) – subset of reaction #1
|
Thus, only 9 of 28 possible combinations (without taking into account the calculated set of 3 linearly independent reactions) provide new dependent reactions in this system, whereas the remaining 19 combinations correspond to already found (degenerate) reactions.
Detection of linear dependency of some reaction on the specified set of linearly independent reactions (IR set) is also based on transformation of the coefficients' matrix of all these reactions to a trapezoidal form: if the tested reaction corresponds to combination of reactions from the IR set, the last row will be nullified after application of the Gauss elimination method.
 Reactions: the program for generation of all possible reactions between specified substances and selection of arbitrary sets of linearly independent reactions
Reactions: the program for generation of all possible reactions between specified substances and selection of arbitrary sets of linearly independent reactions
Comments
Program update
The program has been updated a little: