Аппроксимация линий реакций односегментными параметрическими кубическими кривыми Безье
Однажды при подготовке в CorelDRAW диаграмм, рассчитанных с помощью THERMOCALC, я обнаружил, что почти любая линия реакции может быть представлена всего лишь одним сегментом кубической кривой Безье, причём с очень высокой точностью (погрешность аппроксимации не больше, чем погрешность P–T данных, выводимых программой), например:
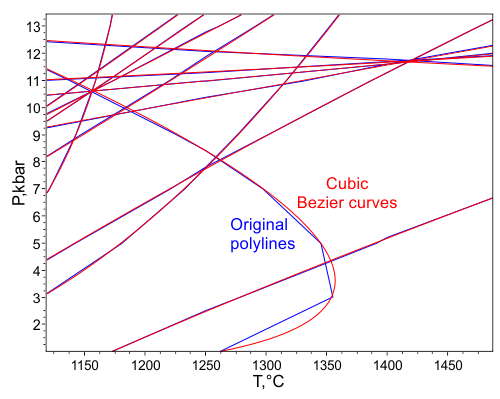
Я подумал, что использование параметрических кубических кривых Безье на диаграммах в TC_Comb (так же, как и в TriQuick) должно быть многообещающим, т.к. эти кривые обладают рядом преимуществ по сравнению с традиционным представлением в виде ломаных линий (а также в виде непараметрических кривых):
- Сглаженные линии должны представлять данные более корректно, особенно если мы имеем дело с пересечениями нескольких кривых в одной точке и пытаемся анализировать увеличенные фрагменты диаграмм;
- Любая односегментная кубическая кривая Безье определяется только 4-мя управляющими точками (т.е. всего 8-ю коэффициентами), что приводит к заметной экономии памяти, в т.ч. к уменьшению объёмов сохраняемых файлов;
- Параметрическая форма уравнения идентична для любой линии реакции, так что можно отказаться от определения наклонов: горизонтальность, вертикальность или сильная изогнутость линий не учитываются при расчётах, данные обрабатывается одинаково для всех вариантов;
- Математические выражения кубической кривой Безье и её производных являются очень короткими и простыми;
- Быстрые и эффективные процедуры для отображения кубических кривых Безье и некоторых операций с ними реализованы в базовых модулях всех операционных систем, использующих графический интерфейс;
- По крайней мере, гладкие кривые выглядят лучше, чем ломаные линии!
Главный же недостаток – это то, что разработка аппроксимационной процедуры является нетривиальной, довольно сложной задачей, а готовый к использованию хороший алгоритм найти трудно: приближение линии кривой Безье – это итерационный процесс, состоящий в чередовании МНК и процедуры репараметризации до достижения требуемой точности аппроксимации. Также сложны в реализации некоторые базовые операции с кривыми Безье, например – поиск их пересечений. Однако, они и не требуются для простой визуализации линий. TC_Comb использует собственный итерационный алгоритм для аппроксимации ломаной линии односегментной кривой Безье, который не является оптимальным, однако в большинстве случаев демонстрирует хорошее качество приближения. Базовые процедуры этого алгоритма взяты из проекта MATHLAB д-ра Муртаза Хана (разработавшего простой и высоко оптимизированный МНК-алгоритм, находящий две промежуточные управляющие точки кубической кривой Безье при фиксированных краевых точках) и из статьи М. Пласса и М. Стоуна (в которой описаны выражения для репараметризации кубической кривой Безье), с некоторыми дополнительными операциями, вроде масштабирования исходных данных, обработки тривиальных случаев и перестановки опорных точек после возникающей иногда в ходе работы смене их порядка. Версия алгоритма, реализованная в TC_Comb, также проверяет отклонение получающейся кривой от исходного набора точек и при обнаружении проблем оставляет представление в виде ломаной линии.
Я здесь также выложил небольшой проект на Delphi 7 для тех программистов-любителей, кого заинтересует эта реализация аппроксимации кривой Безье. Я его использовал на стадии разработки для тестирования алгоритма. Этот проект содержит ещё один алгоритм МНК, предложенный Джимом Герольдом: он находит все 4 управляющих точки сегмента кривой Безье (т.е. положение конечных точек в нём не зафиксировано). Программа записывает TVL-файлы, которые могут быть загружены в программу TriQuick. Вы можете использовать этот проект в качестве отправной точки для собственных разработок (например, если хотите написать собственный более-менее приличный вариант аппроксимации многосегментной кривой Безье).
Источники:
- Dr. Murtaza Khan, 2007-2009. Cubic Bezier least square fitting // Проект MATHLAB. WEB-страница: www.mathworks.com.
- M. Plass & M. Stone, 1983. Curve-fitting with piecewise parametric cubics // SIGGRAPH’83 Proceedings, p. 229–239.
- Jim Herold, 2012. Best Fit Bezier Curve // Интернет-статья опубликована по адресу: https://www.jimherold.com/computer-science/best-fit-bezier-curve; реализация на языке JAVA на сайте SourceForge.
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии