Reactions: программа для вычисления всех возможных реакций между заданными веществами и выделения в них произвольных наборов линейно независимых реакций
Reactions – это небольшая удобная программа, позволяющая быстро вычислять все возможные реакции между заданными веществами (чистыми минералами и компонентами твёрдых растворов, отдельными оксидами и химическими элементами), а также выделять в них произвольные наборы линейно независимых реакций. Программа может пригодиться при исследовании мультисистем и построении петрогенетических сеток, при анализе диаграмм мультиравновесной термобарометрии, для уравнивания предполагаемых реакций с участием минералов реальных составов, для вывода конечных членов твёрдых растворов, а также для образовательных целей.
Несмотря на то, что общий подход к вычислению всех реакций, возможных для заданного набора химических веществ, является довольно простой процедурой и был описан во многих публикациях – например, в монографии Фрэнка Спира (F. Spear, Metamorphic Phase Equilibria and Pressure-Temperature-Time Paths, 1993, глава 5) или в материалах Декстера Перкинса (D. Perkins) на веб-ресурсе Teaching Phase Equilibria, а также используется в таких известных программах, как TWQ (Berman, 1991) и THERMOCALC (Powell & Holland, 1988), – было решено привести достаточно детальное описание алгоритма, используемого в программе Reactions, т.к. он имеет небольшие отличия от общепринятых схем (часть его реализации на Паскале Вы можете найти в документации к программе). Кроме того, большее внимание уделено процедуре генерации линейно зависимых реакций, описываемой обычно весьма скупо. Для наглядности будем сопровождать описание достаточно сложным примером – системой, состоящей из альмандина (Alm), силлиманита (Sill), аннита (Ann), ферросилита (Fs), мусковита (Mu), флогопита (Phl), пиропа (Prp) и кварца (Qtz).
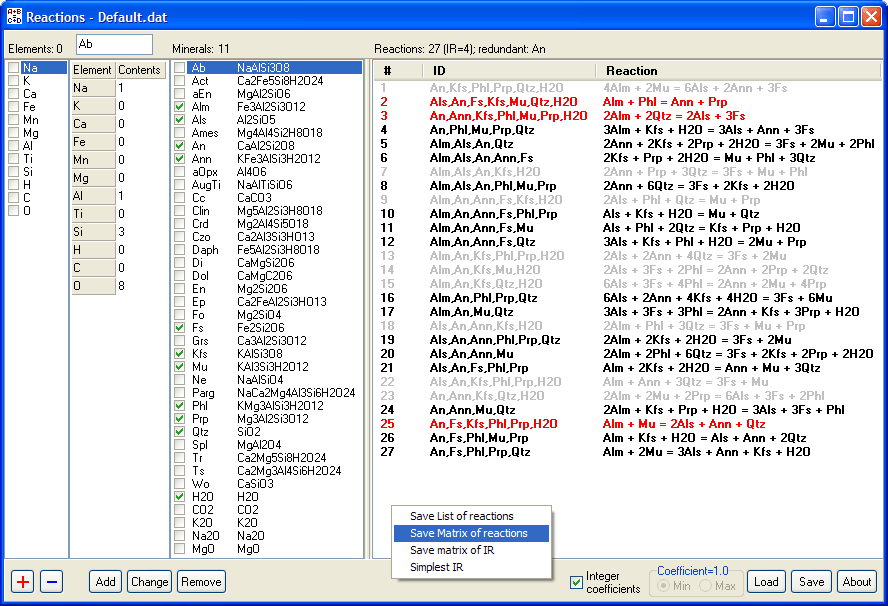
Вычисление реакций осуществляется в несколько этапов.
В первую очередь, составим матрицу составов всех веществ, которые могут участвовать в реакциях:
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Fe | 3 | 0 | 3 | 2 | 0 | 0 | 0 | 0
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| Al | 2 | 2 | 1 | 0 | 3 | 1 | 2 | 0
|
|---|
| Si | 3 | 1 | 3 | 2 | 3 | 3 | 3 | 1
|
|---|
| H | 0 | 0 | 2 | 0 | 2 | 2 | 0 | 0
|
|---|
| O | 12 | 5 | 12 | 6 | 12 | 12 | 12 | 2
|
|---|
Затем с помощью метода исключения переменных Гаусса-Жордана преобразуем её в матрицу приведённого (канонического) ступенчатого вида (RREF – Reduced Row-Echelon Form). Небольшим, но важным отличием от стандартного варианта метода, облегчающим дальнейшую работу, является превращение левой части матрицы в единичную (за счёт перестановки как строк, так и столбцов матрицы). Все операции с матрицами (как в методе Гаусса-Жордана, так и при вычислении коэффициентов линейно зависимых реакций) основаны на простейших эквивалентных преобразованиях:
- Перестановка строк и столбцов
- Умножение строки на константу
- Сложение строк
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 1 | 0.667 | 0 | 0 | 0 | 0 | Fe/3, строка перемещена вверх
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| Al | 0 | 2 | ‑1 | ‑1.333 | 3 | 1 | 2 | 0 | Al-Fe*2
|
|---|
| Si | 0 | 1 | 0 | 0 | 3 | 3 | 3 | 1 | Si-Fe*3
|
|---|
| H | 0 | 0 | 2 | 0 | 2 | 2 | 0 | 0
|
|---|
| O | 0 | 5 | 0 | -2 | 12 | 12 | 12 | 2 | O-Fe*12
|
|---|
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 1 | 0.667 | 0 | 0 | 0 | 0
|
|---|
| Al | 0 | 1 | ‑0.5 | ‑0.667 | 1.5 | 0.5 | 1 | 0 | Al/2, строка перемещена вверх
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| Si | 0 | 0 | 0.5 | 0.667 | 1.5 | 2.5 | 2 | 1 | Si-Al
|
|---|
| H | 0 | 0 | 2 | 0 | 2 | 2 | 0 | 0
|
|---|
| O | 0 | 0 | 2.5 | 1.333 | 4.5 | 9.5 | 7 | 2 | O-Al*5
|
|---|
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 0 | 0.667 | ‑1 | ‑1 | 0 | 0 | Fe-K
|
|---|
| Al | 0 | 1 | 0 | ‑0.667 | 2 | 1 | 1 | 0 | Al+K/2
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| Si | 0 | 0 | 0 | 0.667 | 1 | 2 | 2 | 1 | Si-K/2
|
|---|
| H | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | H-K*2, удалить
|
|---|
| O | 0 | 0 | 0 | 1.333 | 2 | 7 | 7 | 2 | O-K*2.5
|
|---|
| Alm | Sill | Ann | Fs | Mu | Phl | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 0 | 0 | ‑2 | ‑3 | ‑2 | ‑1 | Fe-Si/3*2
|
|---|
| Al | 0 | 1 | 0 | 0 | 3 | 3 | 3 | 1 | Al+Si/3*2
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Si | 0 | 0 | 0 | 1 | 1.5 | 3 | 3 | 1.5 | Si*3/2, строка перемещена вверх
|
|---|
| Mg | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0
|
|---|
| O | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0 | O-Si/3*4
|
|---|
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | Phl перемещён влево
|
|---|
| Fe | 1 | 0 | 0 | 0 | ‑3 | ‑2 | ‑2 | ‑1
|
|---|
| Al | 0 | 1 | 0 | 0 | 3 | 3 | 3 | 1
|
|---|
| K | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0
|
|---|
| Si | 0 | 0 | 0 | 1 | 3 | 1.5 | 3 | 1.5
|
|---|
| Mg | 0 | 0 | 0 | 0 | 3 | 0 | 3 | 0
|
|---|
| O | 0 | 0 | 0 | 0 | 3 | 0 | 3 | 0
|
|---|
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 0 | 0 | 0 | ‑2 | 1 | ‑1 | Fe+Mg*3
|
|---|
| Al | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 1 | Al-Mg*3
|
|---|
| K | 0 | 0 | 1 | 0 | 0 | 1 | ‑1 | 0 | K-Mg
|
|---|
| Si | 0 | 0 | 0 | 1 | 0 | 1.5 | 0 | 1.5 | Si-Mg*3
|
|---|
| Mg | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | Mg/3
|
|---|
| O | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | O-Mg*3, удалить
|
|---|
В результате получается трапециевидная матрица, содержащая только линейно независимые строки (отвечающие элементам) с квадратной единичной левой частью и прямоугольной правой частью, уже отвечающей коэффициентам уравнений некоторого набора линейно независимых реакций (для данной системы – трёх):
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz
|
|---|
| Fe | 1 | 0 | 0 | 0 | 0 | ‑2 | 1 | ‑1
|
|---|
| Al | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 1
|
|---|
| K | 0 | 0 | 1 | 0 | 0 | 1 | ‑1 | 0
|
|---|
| Si | 0 | 0 | 0 | 1 | 0 | 1.5 | 0 | 1.5
|
|---|
| Mg | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0
|
|---|
Таким образом, для получения матрицы коэффициентов этого набора линейно независимых реакций достаточно просто транспонировать правую прямоугольную часть полученной матрицы, дополнив её справа отрицательной единичной матрицей:
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz
|
|---|
| ‑2 | 3 | 1 | 1.5 | 0 | ‑1 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑1 | 1 | 0 | 1.5 | 0 | 0 | 0 | ‑1
|
Или с целочисленными коэффициентами (умножив строки на соответствующие константы):
| Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0 | 1 | 4Alm+2Mu=6Sill+2Ann+3Fs | (Phl,Prp,Qtz)
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0 | 2 | Ann+Prp=Alm+Phl | (Sill,Fs,Mu,Qtz)
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2 | 3 | 2Alm+2Qtz=2Sill+3Fs | (Ann,Phl,Mu,Prp)
|
Все последующие вычисления производятся только с этой небольшой матрицей коэффициентов линейно независимых реакций.
В последнем столбце таблицы с коэффициентами реакций приведены те вещества системы, которые в данной реакции не участвуют: так принято обозначать реакции в мультисистемах. Следует отметить, что эта система обозначений играет ключевую роль при вычислении всех остальных возможных реакций в системе, являющихся комбинациями полученного небольшого набора линейно независимых реакций, т.к. при комбинировании реакций требуется приводить к нулю коэффициенты именно этих, отсутствующих в реакциях веществ.
Судя по преобразованной матрице составов можно утверждать, что максимальное число веществ M, участвующих в реакции, должно быть на 1 больше числа независимых элементов (строк) E, т.е. M=E+1. Для данной системы M=5+1=6. Из этого следует, что число отсутствующих в реакциях веществ системы N не может быть меньше общего числа веществ Q за вычетом этого максимального числа веществ M, т.е. N=Q-E-1. Для данной системы N=8-5-1=2.
Процедура вычисления линейно зависимых реакций основана на переборе всех возможных сочетаний по N веществ из их общего количества Q. Общее число таких комбинаций C определяется по формуле:
$$C = \frac{Q!}{M! \times N!}$$
Для данной системы необходимо перебрать и проверить 28 комбинаций: по 2 вещества при их общем количестве 8. Однако, во всех линейно независимых реакциях полученного набора количества отсутствующих веществ (N) больше двух (3 и 4) за счёт так называемого "вырождения": исключения веществ вследствие подходящих стехиометрических соотношений. Вырождение приводит к тому, что одной реакции отвечают сразу несколько комбинаций, т.е. количество реакций оказывается существенно меньше общего числа комбинаций. Вместе с тем, нет необходимости вычислять коэффициенты для каждой потенциальной реакции: достаточно лишь проверить, не является ли список отсутствующих веществ очередной комбинации подмножеством аналогичного списка одной из уже вычисленных ранее реакций. Если он оказывается таковым, то данная реакция уже существует и комбинация пропускается. Поэтому желательно, чтобы запись каждой реакции содержала, кроме номеров веществ и их коэффициентов в реакциях, также структуру данных и функции для эффективной работы с множествами (например, основанные на массивах битовых масок).
Вычисление коэффициентов линейно зависимых реакций производится преобразованием полученной матрицы коэффициентов набора линейно независимых реакций: сначала перестановкой в начало матрицы тех столбцов, которые отвечают веществам, отсутствующим в реакции, а затем приведением матрицы к трапециевидной форме методом Гаусса. Последний отличается от метода Гаусса-Жордана лишь тем, что левая треугольная часть матрицы не приводится к единичной матрице, т.е. значения выше её главной диагонали могут быть ненулевыми, а на самой главной диагонали – не равными 1. В результате в первых столбцах последней строки (под главной диагональю треугольной части матрицы) окажутся только нулевые значения, т.е. последняя строка будет содержать коэффициенты искомой реакции (которые останется лишь привести к целым числам). Первый шаг стоит оптимизировать, оперируя не самими столбцами, а только лишь их порядковыми номерами.
Итак, вычислим с помощью этого алгоритма все оставшиеся линейно зависимые реакции нашей системы:
| Комбинация | Отсутствующие вещества | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| 1 | (Alm,Sill) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| -2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | 0 | ‑1.333 | 2 | 0.667 | 0.667 | ‑0.667 | ‑2
|
|
| 0 | 0 | ‑2 | 3 | 1 | 1 | ‑1 | ‑3 | 4 | 2Ann+Prp+3Qtz=3Fs+Phl+Mu | (Alm,Sill)
|
| Комбинация | Отсутствующие вещества | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| 2 | (Alm,Ann) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑4 | 0 | 0 | ‑2 | 2 | 2 | ‑2
|
|
| 0 | ‑2 | 0 | 0 | ‑1 | 1 | 1 | ‑1 | 5 | 2Sill+Phl+Qtz=Mu+Prp | (Alm,Ann,Fs)
|
|
| 3 | (Alm,Fs) – подмножество реакции №5
|
| Комбинация | Отсутствующие вещества | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| 4 | (Alm,Phl) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| 0 | ‑2 | ‑2 | 3 | 0 | 2 | 0 | ‑4 | 6 | 2Sill+2Ann+4Qtz=3Fs+2Mu | (Alm,Phl,Prp)
|
| Комбинация | Отсутствующие вещества | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| 5 | (Alm,Mu) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | 2 | ‑2 | 3 | 2 | 0 | ‑2 | ‑2 | 7 | 2Ann+2Prp+2Qtz=2Sill+3Fs+2Phl | (Alm,Mu)
|
|
| 6 | (Alm,Prp) – подмножество реакции №6
|
| Комбинация | Отсутствующие вещества | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| 7 | (Alm,Qtz) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 0 | ‑1 | ‑1 | 1.5 | 0 | 1 | 0 | ‑2
|
| 0 | 1.5 | ‑0.5 | 0.75 | 1 | ‑0.5 | ‑1 | 0
|
|
| 0 | 6 | ‑2 | 3 | 4 | ‑2 | ‑4 | 0 | 8 | 2Ann+2Phl+4Prp=6Sill+3Fs+4Phl | (Alm,Qtz)
|
| Комбинация | Отсутствующие вещества | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| 8 | (Sill,Ann) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑0.667 | 0 | ‑0.667 | 2 | 0 | 0.667 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑1.333 | 0 | 0 | 2 | ‑0.667 | 0.667 | 0.667 | ‑2
|
|
| ‑2 | 0 | 0 | 3 | ‑1 | 1 | 1 | ‑3 | 9 | 2Alm+Phl+3Qtz=3Fs+Mu+Prp | (Sill,Ann)
|
|
| 9 | (Sill,Fs) – подмножество реакции №2
|
| Комбинация | Отсутствующие вещества | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| 10 | (Sill,Phl) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑0.667 | 0 | ‑0.667 | 2 | 0 | 0.667 | 0 | ‑2
|
|
| ‑1 | 0 | ‑1 | 3 | 0 | 1 | 0 | ‑3 | 10 | Alm+Ann+3Qtz=3Fs+Mu | (Sill,Phl,Prp)
|
|
| 11 | (Sill,Mu) – подмножество реакции №2
|
| 12 | (Sill,Prp) – подмножество реакции №10
|
| 13 | (Sill,Qtz) – подмножество реакции №2
|
| 14 | (Ann,Fs) – подмножество реакции №5
|
| 15 | (Ann,Phl) – подмножество реакции №3
|
| 16 | (Ann,Mu) – подмножество реакции №3
|
| 17 | (Ann,Prp) – подмножество реакции №3
|
| Комбинация | Отсутствующие вещества | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| 18 | (Ann,Qtz) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| ‑1 | 3 | 0 | 1.5 | 1 | ‑1 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
| ‑1 | 3 | 0 | 1.5 | 1 | ‑1 | ‑1 | 0
|
|
| ‑2 | 6 | 0 | 3 | 2 | ‑2 | ‑2 | 0 | 11 | 2Alm+2Mu+2Prp=6Sill+3Fs+2Phl | (Ann,Qtz)
|
| Комбинация | Отсутствующие вещества | Alm | Sill | Ann | Fs | Phl | Mu | Prp | Qtz | № | Реакция | Отсутствующие вещества
|
|---|
| 19 | (Fs,Phl) | ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| ‑2 | 2 | 0 | 3 | 0 | 0 | 0 | ‑2
|
|
| ‑4 | 6 | 2 | 3 | 0 | ‑2 | 0 | 0
|
| 1 | 0 | ‑1 | 0 | 1 | 0 | ‑1 | 0
|
| 2 | ‑4 | ‑2 | 0 | 0 | 2 | 0 | ‑2
|
|
| 1 | ‑2 | ‑1 | 0 | 0 | 1 | 0 | ‑1 | 12 | 2Sill+Ann+Qtz=Alm+Mu | (Fs,Phl,Prp)
|
|
| 20 | (Fs,Mu) – подмножество реакции №2
|
| 21 | (Fs,Prp) – подмножество реакции №12
|
| 22 | (Fs,Qtz) – подмножество реакции №2
|
| 23 | (Phl,Mu) – подмножество реакции №3
|
| 24 | (Phl,Prp) – подмножество реакции №10
|
| 25 | (Phl,Qtz) – подмножество реакции №1
|
| 26 | (Mu,Prp) – подмножество реакции №3
|
| 27 | (Mu,Qtz) – подмножество реакции №2
|
| 28 | (Prp,Qtz) – подмножество реакции №1
|
Таким образом, в этой системе из 28 возможных комбинаций (без учёта вычисленного набора из 3-х линейно независимых реакций) только 9 дают новые линейно зависимые реакции, тогда как остальные 19 комбинаций отвечают уже найденным (вырожденным) реакциям.
Определение линейной зависимости некоторой реакции от некоторого набора линейно независимых реакций также осуществляется приведением матрицы коэффициентов всех этих реакций к трапециевидной форме: если тестируемая реакция является линейно зависимой, то последняя строка матрицы после применения метода Гаусса оказывается нулевой (и может быть сокращена).
Комментарии
Program update
The program has been updated a little: